Theories 5-8
This guide is currently undergoing change. Keep in mind, strategies may change.
Graduation routing #
Remember to follow our routing advice from the introduction to graduation.
| 9k | → | 9.4k | → | 9.8k | → | 10k |
| 10k | → | 10.4k | → | 10.6k | → | 11k |
| 11k | → | 12.4k | → | 13.4k | → | 14k |
| Skip T8 | ||||||
| 14k | → | 14.8k | → | 15.6k | → | 16k |
| 16k | → | 16.8k | → | 18k | ||
| 18k | → | 20k |
Student routing with R9 #
All routing follows the student calculator (by Niedzielan, AfuroZamurai, and Milla) and star calculator (by Eaux Tacous#1021). When you are not pushing \(f(t)\) you should always have the 9th research option maxed (after Theory 8). When pushing \(f(t)\), you should be R9 seaping (below).
There is also the theory simulator by XLII, which works both below max milestones and after max milestones for all theories.
How to push F(t) with R9 swapping #
Memorize your student distributions with and without 10/20/30 R9 students. Use the student calculator if needed. You will commonly see people refer to this as R9 seaping as a long held name of the strategy.
- Wait till \(f(t)\) stops growing with students in R9 pushing \(\tau\).
- Start accel (preferably keep it between prestiges).
- Potentially sit here to stack t for bigger \(\varphi_2\) when you have students in \(\varphi_2\). Only do this when you are near a graduation mark. This is not useful if you will not swap into \(\varphi_2\).
- Respec all 10/20/30 students from R9.
- Wait for the autoprestige to prestige and swap back students to R9.
- Repeat.
This method allows you to push \(f(t)\) with almost no loss of R9 uptime or pushing power. This is harder with fewer levels of R9 but still helps if you get used to it.
R9 autoprestige expression #
You can find the autoprestige used for R9 Seaping here: Equation. If you don’t have this expression, then you will have to manually prestige each seap.
Reference R9 Swapping Autoprestige Explanation
Theory 1 #
You will not touch this theory until after ee14k. Once you begin pushing T1 after ee14k, begin using the Theory Sim and the Theory Sim Guide to give the best strategy and multiplier for the next publication.
Theory 2 #
This theory will be used as overnight until 1e350 Tau where it will not be touched until after ee14k. See our earlier guide for an overview for theory 2.
Theory 3 #
See our earlier guide for an overview for theory 3.
Theory 4 #
See our earlier guide for an overview for theory 4.
Theory 5 (40σ / 9k) #
Variable overview #
\(q_1\) & \(q_2\): Simple multipliers that directly affect \(\rho\) production. \(q_2\) is a doubling while \(q_1\) is not.
\(q\): The crux of T5 is to grow this value as fast as possible, while increasing its maximum value.
\(c_1\): Increases the speed that \(q\) will approach its limit. You need enough levels of \(c_1\) to allow \(q\) to reach its limit, once \(q\) has reached its cap \(c_1\) has no additional benefit until more \(c_2\) is purchased.
\(c_2\): Doubles the limit of \(q\) and halves the effect of \(c_1\). Needed to balance 2 parts of the equation appearing twice: \(c_1/c_2\) and \(c_3^{1.1}-q/c_2\). If you buy too much \(c_2\), it will make \(q\) growth effectively nothing as \(c_1/c_2\) approaches \(0\). However, you still need to buy \(c_2\) when \(q\) approaches \(c_2*c_3^{1.1}\) because \(c_3^{1.1}-q/c_2\) approaches \(0\) making \(q=c_2*c_3^{1.1}\) the maximum value of \(q\).
\(c_3\): Increases the limit of \(q\) by \(2^{1+m/20}\), where \(m\) is the number of milestones, by increasing what \(q/c_2\) fraction can reach. It does not have the problems of \(c_2\) as lowering your \(\dot{q}\), making it an always auto-bought variable.
T5 strategy #
Theory 5 benefits the most from active play and a lot of attention making it the strongest theory until the very late game due to a very low multiplier decay rate. Here is what is known about optimal multiplier: \(3\) until \(e25\); \(6\) to \(10\) during mid to late game. Publishing at higher multiples is not drastically less efficient and allows for slightly less active play. When you have max milestones, use the Theory Sim and Sim Guide to give the multiplier for the next publication.
Active
Running the active strats, with some modifications, will help you get this theory to \(e30\) easily, but it will take some time. A step-by-step on how to progress the theory is detailed below.
Before e30, you should repeat this after every publication:
- Buy everything except \(c_2\).
- Once \(q\) growth reduces, \(c_2\) levels can then be purchased individually. Only buy when \(c_2\) is \(e1\) lower than your current \(\rho\).
- When you are within \(e10\) of your last publication, autobuy all but \(q_1\) & \(c_1\). You should then manually buy \(q_1\) and \(c_1\) when it costs \(e1\) lower than the \(q_2\) doubling. Buy \(c_1\) only when \(q\) is not capped.
- Repeat until \(e25\). At \(e25\), push for \(e30\) with 0/1/0 milestone and start \(x6-10\) multipliers.
After autobuy at e30, you should repeat this after every publication:
- x1 (or x10 when above e200) buy \(c_2\) manually and autobuy the rest until within ~e10 of your previous publication. Your graph should resemble a linear function on the graph.
- Around your last pub mark within ~\(e10\), start autobuying \(c_2\) and stop autobuying \(c_1\) & \(q_1\). At this point:
- buy \(q_1\) up to \(15\%\) of the cost of the next doubling purchase (\(2^x\) purchase),
- and buy \(c_1\) after you purchase \(c_2\) up to \(e1\) lower than \(q\).
- Once you reach the desired publication point, publish.
- Repeat this for stonks.
Commentary
No commentary
T5 will always give its best results from active play. However, after step 3, you can still get good results while autobuying \(q_1\) and manually purchasing \(c_1\) every 10-15min. This makes the theory slightly less active and easier to deal with.
Warning: Do not overnight this theory. It has terrible decay after passing a good publication mark and will not give good results. T5i is only viable very late/endgame.
T5 milestone route #
| 0/1/0 | → | 3/1/0 | → | 3/1/2 |
| Or | ||||||
| 2 | → | 1 x3 | → | 3 x2 |
Additional information
Purchase \(c_2\) when \(1.5q > c_2*c_3^{m_3}\). \(m_3\) is the number of milestone 3.
\(q\) begins to slow down when you reach \(2q > c_2*c_3^{m_3}\).
Strategy constructed by: Snaeky, Marks, Baldy, and Nerdy
Theory 6 (45σ / 10k) #
T6 strategy #
This theory has the lowest decay of all the theories. It will be second place to T5 until about e750 and is the only theory that can get to \(>e1100τ\). You should overnight this after you get your T2 to \(e350+\). This is the best idle theory. Video of T6 at Endgame
The optimal publication multiplier is still unknown but empirically seems to be about \(7\)-\(12\). Once all milestones, disable \(c_3\) \(c_4\) and autobuy rest. For manual autobuy \(q_2\), \(r_2\), \(c_2\), and \(c_5\) then manual buy rest with \(c_3\) and \(c_4\) still disabled. For idle/auto, you are going to just turn off \(c_3\) and \(c_4\).
T6 milestone route #
| 0/0/0 | → | 0/1/0 | → | 1/1/0/0 |
| 1/1/0/0 | → | 1/1/1/0 | → | 1/0/0/3 |
| 1/0/0/3 | → | 1/0/1/3 | → | 1/1/1/3 |
| Or | ||||||
| 2 | → | 1 | → | 3 | ||
| 3 | → | 4 {2&3→4} | → | 3 | → | 2 |
Theory 7 (50σ / 11k) #
T7 overview #
T7 can be summarized as a maximization problem : given a surface in 3-dimensional space, you want to find its highest altitude by moving along the surface, always in the direction of steepest ascent (that’s basically a gradient ascent). The function \(g(x,y)\) can be seen as a surface in \(\mathbb{R}^{3}\) (considering the set of points \((x,y,g(x,y))\), see attached image). \((\rho_1,\rho_2,g(\rho_1,\rho_2))\) is a point on this surface. Our goal is to maximize \(g(\rho_1,\rho_2)\), i.e. to find \((\rho_1,\rho_2)\) that maximize \(g(\rho_1,\rho_2)\). Notice that the function \(g\) is unbounded, i.e. you can’t find a proper maximum (we say that the maximization problem is ill-conditioned); so one way to maximize \(g(\rho_1,\rho_2)\) is to move \((\rho_1,\rho_2)\) towards the direction of steepest ascent. This is what is precisely done by setting \(\dot{\mathbf{\rho}}\) (which is the direction the point \(\mathbf{\rho}=(\rho_1,\rho_2)\) will move toward) to \(\nabla g(\rho_1,\rho_2)\) (i.e. the gradient of \(g\) evaluated at \((\rho_1,\rho_2)\), which gives the direction of steepest ascent of \(g\) at the point \((\rho_1,\rho_2)\).
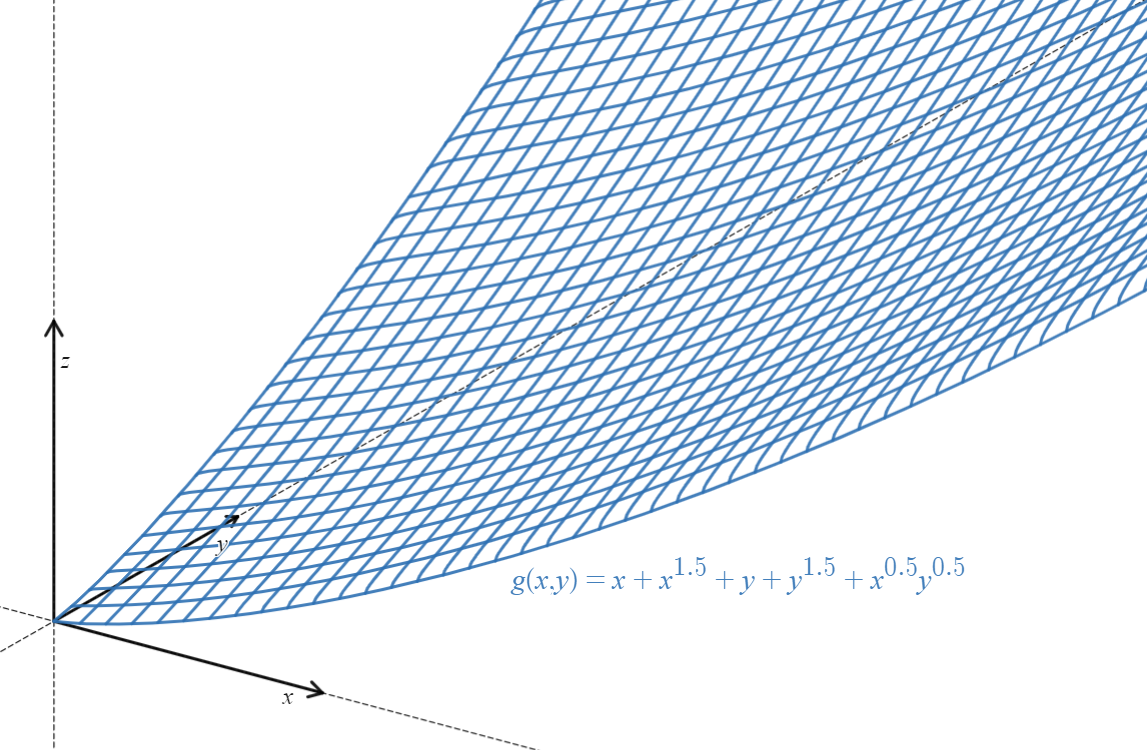
This is the graph of the function \(g\), taken after the first four milestones have been unlocked (Note: here, coefficients like \(c_1,c_2\ldots\) are ignored. The effect of those coefficients is simply making the graph steeper in \(x\) or \(y\) direction, depending on the value of each coef).
T7 strategy #
The optimal publication multiplier is \(4\)-\(6\). You will swap from 0/1/1 → 0/0/2 at near the 2/3 mark of your next milestone. The strategy for manual buy before 4 milestones is to only manual buy \(q_1\) and \(c_1\) cheap (e1 less \(\rho\)) and the rest full auto. After milestone 5, turn it on full autobuy for idle. For active, you will follow the strat described in the theory sim guide or watch the video below.
T7 milestone route #
| 0/0/0 | → | 0/1/0 | → | 0/1/1 |
| 0/1/1 | → | 0/0/2 | → | 0/0/3 |
| 0/0/3 | → | 0/1/3 | → | 1/1/1/1/1 |
| 1/1/1/1/1 | → | 1/1/1/1/2 | → | 1/1/1/1/3 |
| Or | ||||||
| 3 | → | 3 | → | 3 | ||
| 2 | → | 1 {5→3&4} | → | 3 | ||
| 3 | → | 2 |
Theory 8 skipping #
T8 skip is significantly faster than buying T8 right away (don’t worry, you will still buy it, just at 14k, not 12k). T8 is very slow until you get to about \(e60\) (it took the sim 16 hours to get that far into the theory without R9). We highly recommend buying t8 for the achievement, then selling it right away and using those students for \(\varphi\). You will need about e1350 \(\tau\) in order to get R9 (\(ee14k\)) without T8, which will help you get through T8 faster than before. You will need to buy T8 again to get R9, and you should start R9 right away after that The current recommendation for your \(\tau\) distribution for T8 skip is as follows:
| Tau | Tau | |||
|---|---|---|---|---|
| T1 | e200 τ | T5 | e250 τ | |
| T2 | e275 τ | T6 | e150 τ | |
| T3 | e150 τ | T7 | e150 τ | |
| T4 | e175 τ | T8 | Skip |
If your numbers are different, that is fine. You just need to reach 1e1350 \(\Pi\tau\) to get to R9 at 14k.
Theory 8 (55σ / 12k) #
T8 strategy #
The optimal publication multiplier is 2.5-5 depending on how close you are to the next milestone. This theory is extremely slow at the start which is why we skip until we obtain R9. It is also the only one with a \(1e20\) milestone step. It will speed up once you hit \(1e60\) and even faster at \(1e80\) and \(1e100\) etc. until ~\(e250\)-\(e300\). The worst part is the \(1e50\)-\(1e60\) grind. The grind to \(1e60\) will take a good bit of time but is faster with R9.
At the start, manual buy prioritizes \(c_2\) then \(c_1\) then rest. Once you get to 0/0/0/2, prioritize \(c_2\) and \(c_5\) then \(c_1\) then the rest. Once at 2/0/3/0, you will prioritize \(c_2\) and \(c_4\) then \(c_1\) then the rest after. This continues to max at 2/3/3/3.
| Starting Positions | Time Step | |
|---|---|---|
| Lorenz | (-6, -8, 26) | 0.02 |
| Chen | (-10.6, -4.4, 28.6) | 0.002 |
| Rossler | (-6, 15, 0) | 0.00014 |
T8 milestone route #
| 0/0/0/0 | → | 1/0/0/0 | → | 2/0/0/0 |
| 2/0/0/0 | → | 0/0/0/2 | → | 0/0/0/3 |
| 0/0/0/3 | → | 1/0/0/3 | → | 2/0/3/0 |
| 2/0/3/0 | → | 2/3/3/0 | → | 2/3/3/3 |
| Or | ||||||
| 1x2 | → | {1→4} | → | 4 | ||
| 4 | → | 1 | → | 1 {4→3} | → | 1 |
| 1 | → | 2 x3 | → | 4 x3 |
Note: the 2/0/0/0 → 0/0/0/2 swap happens at e52 tau.